Perché serve conoscere il valore di g?

Fig. 1

Absolute gravity measurement apparatus, developed in 1976 at the Earthquake Research Institute, Japan – National Museum of Nature and Science, Tokyo – DSC07819.JPG

Dal Dizionario delle Scienze Fisiche della Treccani leggiamo cosa significa il termine “gravimetria”:

“Parte della geofisica che considera le teorie e i metodi di osservazione destinati allo studio del campo gravitazionale terrestre e alla misurazione dell’accelerazione di gravità g. L’accelerazione di gravità sulla superficie terrestre può essere misurata in modo assoluto o relativo.

La misura assoluta, effettuata in alcune località dette stazioni gravimetriche fondamentali, corrisponde al valore dell’effettiva accelerazione di un oggetto in caduta libera nel vuoto.

La misura relativa fornisce la differenza fra i valori registrati dalle stazioni di misura e viene effettuata con strumentazione meno sofisticata allo scopo di determinare le anomalie di gravità.”

Perché è importante la determinazione del valore di g? Quali sono le applicazioni?

Gli studi gravimetrici hanno fra i principali scopi l’individuazione di giacimenti petroliferi, lo studio tettonico e geodinamico, lo studio dei bacini sedimentari, le indagini archeologiche e sul rischio vulcanico e la misurazione dello spessore dei ghiacci polari.

L’attività prospettiva, cioè la misurazione, può effettuarsi sul terreno, in mare o tramite un aereo o elicottero ed ha come scopo quello di individuare eventuali anomalie della gravità, cioè delle divergenze locali dell’accelerazione di gravità dai corrispondenti valori “normali”. 

Dalla scoperta di tali anomalie di g in un determinato luogo, si possono avere indicazioni molto importanti sulla densità locale del terreno e quindi sulla presenza di giacimenti minerari o petroliferi o per lo studio dell’orbita dei satelliti artificiali.

Dalle osservazioni temporali di g in zone vulcaniche è possibile studiare lo spostamento delle masse magmatiche sottostanti. 

I dati gravimetrici sono utilizzati, inoltre, per studiare i movimenti relativi di placche continentali e le variazioni del livello medio dei mari.

La conoscenza accurata di g è necessaria non solo in metrologia per la definizione di grandezze fisiche, ma anche nella taratura e nell’utilizzo degli strumenti di pesatura che sfruttano la misura della forza-peso; si contribuisce così alla tutela del consumatore. 

Per moltissimo tempo lo strumento fondamentale della gravimetria assoluta è stato il pendolo semplice, poiché l’accelerazione di gravità g è legata alla lunghezza L e al periodo T delle sue piccole oscillazioni. 

Ovviamente il funzionamento degli attuali gravimetri portatili sfrutta altri principi, ma è sempre utile conoscere la storia che sta alle spalle degli strumenti più moderni.

Il nostro vecchio pendolo semplice!

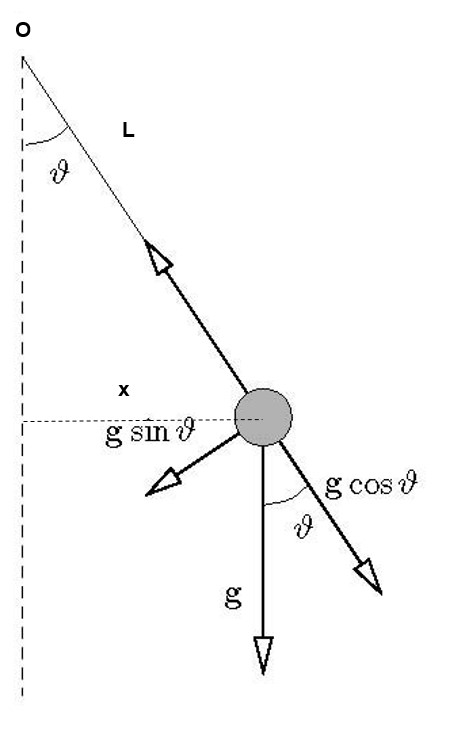
Fig. 2

In figura è rappresentato il vettore g con le sue due componenti, una in direzione parallela al filo di lunghezza L, l’altra parallela allo spostamento della massa che è in movimento.

Possiamo calcolare il momento torcente che deriva dall’azione del peso della massa usando la formula:

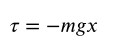
Il momento è calcolato rispetto al punto di sospensione del pendolo O, la forza agente è la forza peso, x è il braccio della forza.

Poiché si devono considerare solo piccole oscillazioni con ϑ ≈ 5°-6° possiamo approssimare l’arco percorso dalla massa con il segmento di lunghezza x

in cui l’angolo ϑ è espresso in radianti.

Il momento torcente si scrive come

Dalla dinamica dei moti rotatori il momento torcente può essere scritto in funzione del momento d’inerzia I e dell’accelerazione angolare 𝛂 del corpo

L’oscillazione di m dipende dalla componente del peso, parallela alla traiettoria

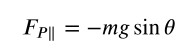
Ma per piccole oscillazioni

Da un punto di vista rigoroso è bene ricordare che lo sviluppo di Taylor del seno al primo ordine è dato da

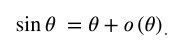
Possiamo scrivere, quindi, 

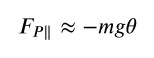
E ricordando che

otteniamo

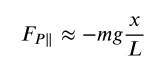
che diventa

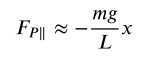
relazione confrontabile con la legge di Hooke, in cui compare la costante elastica k, sostituita in questo caso da

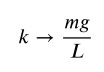
Nel caso di un oscillatore armonico, il periodo di una massa in sospensione ad una molla, è dato dalla relazione:

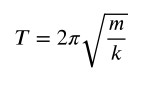
Nel caso del pendolo si ottiene: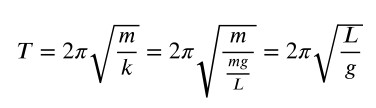

Dall’ultima relazione si ricava il valore dell’accelerazione di gravità g

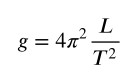
Cosa significa questa legge?

Significa che preso un pendolo di lunghezza L quanto più è grande l’intensità del campo gravitazionale g, tanto minore sarà il suo periodo di oscillazione, ovvero sarà maggiore la frequenza con cui oscilla. 

Ora nota la teoria del pendolo semplice possiamo dedicarci all’attività sperimentale.

Non resta che suggerire la visione di due video di Random Physics canale di Gabriele Battistotti, laureato in Fisica e professore di Matematica e Fisica in una scuola superiore di Bolzano. 

https://youtu.be/q9VQ4JSLJa8 Come misurare la GRAVITÀ con un LIMONE

https://youtu.be/CONLRBuuNqk  Come oscilla un PENDOLO su GIOVE?

Sperimentate ragazzi, sperimentate! Buona FISICA!